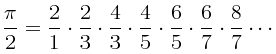Ο Γκότφριντ Βίλχελμ Λάιμπνιτς (Gottfried Wilhelm Leibnitz), που γεννήθηκε την 1 Ιουλίου 1646 στη Λειψία και πέθανε στις 14 Νοεμβρίου 1716 στο Αννόβερο, ήταν Γερμανός φιλόσοφος και επιστήμονας, μαθηματικός, διπλωμάτης, φυσικός, ιστορικός, βιβλιοθηκονόμος και διδάκτορας της Νομικής. Ο Λάιμπνιτς θεωρείται ως το καθολικό πνεύμα της εποχής του (homo universalis): έχει αποκληθεί «ο πολυμαθέστερος άνδρας μετά τον Αριστοτέλη»). (Πηγή: Wikipedia)
Τρία χρόνια περίπου μετά την σειρά του τόξου εφαπτομένης του Gregory, δηλαδή τη σειρά:
(1)
ο μεγάλος Γερμανός Μαθηματικός και Φιλόσοφος Gottried Wilhelm Leibniz (1646-1716), διατύπωσε την ίδια σειρά τόξου εφαπτομένης και στη δημοσίευσή της το 1682, εισάγοντας στη σειρά την τιμή 1 για το x, έδωσε για το π/4 την σειρά:
(2)
από την οποία εύκολα βλέπει κανείς ότι:
(3)
Η σειρά λοιπόν των Gregory-Leibniz, παρά την εντυπωσιακή απλότητά της και παρά την πληροφόρηση που μας παρέχει για το π, στην ουσία είναι άχρηστη σ' ότι έχει να κάνει με τον υπολογισμό των ψηφίων του π. Αυτό γιατί η σειρά συγκλίνει εξαιρετικά αργά. Έτσι για τον υπολογισμό μόνο δύο δεκαδικών ψηφίων του π, απαιτούνται 300 όροι της σειράς, ενώ πρέπει να υπολογίσει κανείς αρκετές χιλιάδες ή και εκατομμύρια όρους για να αποκτήσει η σειρά κάποια χρησιμότητα.
Η σχέση (3), γράφεται επίσης:
Για n = 300, παίρνουμε την τιμή:
π =3,14491,
η οποία είναι “χειρότερη” από την προσέγγιση 3 και 1/7 του Αρχιμήδη.
Για n = 1000, προκύπτει η τιμή:
π= 3,14259
Ενώ τέλος για n =1000000 όρους, έχουμε :
π=3,1416
(Να θυμηθούμε ότι: π = 3,141592653...)
Προκαλεί έκπληξη το γεγονός ότι ο Gregory δεν προσπάθησε να κάνει την αντικατάσταση x =1 στη σειρά του, έτσι ώστε να οδηγηθεί στον απλό τύπο (3) για το π. Πουθενά δεν χρησιμοποιεί ένα τέτοιο υπολογισμό. Μάλλον όμως θα πρέπει να θεωρηθεί απίθανο να μην είχε παρατηρήσει την συγκεκριμένη εφαρμογή, με δεδομένο μάλιστα ότι είχε ασχοληθεί με την υπερβατικότητα του π. Είναι πολύ πιθανό να είχε παρατηρήσει ότι η σειρά του συγκλίνει πολύ αργά, ο ίδιος άλλωστε είχε εισάγει την έννοια της σύγκλισης. Έτσι λοιπόν είναι πολύ πιθανό να θεώρησε ότι δεν άξιζε τον κόπο να κάνει την συγκεκριμένη αναφορά.
Λίγα Μαθηματικά:
Από τα μαθήματα της τριγωνομετρίας στο Λύκειο γνωρίζουμε ότι η εφαπτομένη των 45 μοιρών είναι ίση με την μονάδα. Επίσης, μια “πλήρης” γωνία αντιστοιχεί σε 360 μοίρες ή 2π ακτίνια. Έτσι λοιπόν οι 45 μοίρες αντιστοιχούν σε π/4 ακτίνια. Επομένως στη σχεση (1), βάζοντας x = 1 έχουμε ότι: arctan(1) = 1-1/3+1/5-1/7+1/9-1/11+... Επίσης arctan(1) = π/4. Οπότε τελικά: π/4 =1-1/3+1/5-1/7+1/9-1/11+...
Βιβλιογραφία - Αναφορές
David Blatner, Η χαρά του π, (μετάφραση του: The joy of π), εκδόσεις Ωκεανίδα, Αθήνα 2001
http://www.thefullwiki.org/Archimedes
Η ιστορία του π, Παρασκευή Αρώνη, Μεταπτυχιακή Διπλωματική εργασία, http://www.math.uoa.gr/me/dipl/dipl_aroni.pdf
Γιάννης Φιορεντίνος
ΠΕ 04, ΜΔΕ Προχωρημένες Σπουδές στη Φυσική
(38) Συνεχίζεται...

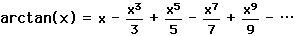
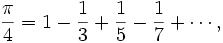






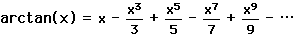
 (2)
(2)