Στη
διάρκεια του δέκατου έβδομου αιώνα
έζησαν και πολλοί άλλοι σπουδαίοι
μαθηματικοί, όπως ο Blaise
Pascal,
o Johannes
Kepler,
o Bonaventura
Cavalieri,
o Pierre
de Fermat,
οι
οποίοι εκτός των άλλων συνεισφορών τους
πλησίασαν αρκετά τις ιδέες του επερχόμενου
απειροστικού λογισμού.


Ένας
ακόμη μαθηματικός που συνεισέφερε
σημαντικά στη διερεύνηση του π αλλά
και στην εξέλιξη του απειροστικού
λογισμού είναι και ο James
Gregory
(1638-1675). Πριν
τον πρόωρο θάνατό του (το 1675 σε ηλικία
μόλις 36 ετών), βρήκε μια απλή και έξυπνη
λύση για τον υπολογισμό του τόξου της
εφαπτομένης [τοξεφ(χ)
ή arctan(x)],
δηλαδή
τη σειρά του τόξου εφαπτομένης, που
φέρει και το όνομά του:
(σειρά
του Gregory)
O
Gregory ανακάλυψε ότι το εμβαδόν της
επιφάνειας που βρίσκεται κάτω από τη
γραφική παράσταση της συνάρτησης
1/(1+χ^2) , στο διάστημα (0,1) είναι ίσο με
τοξεφ(χ) ή arctan(x). Στη
συνέχεια χρησιμοποιώντας τον τύπο του
Cavalieri κατέληξε στη φερώνυμη
σειρά του για το τοξεφ(χ).Βρήκε δηλαδή
αυτό που σήμερα γράφουμε ως:
Η
σειρά λοιπόν (1) του Gregory
διατυπώθηκε το 1671 και σήμανε την
απαρχή μιας νέας εποχής για τον υπολογισμό
του π. Τη σχέση έχει όμως η εν λόγω σειρά
με το π; Η απάντηση είναι πολύ απλή. Αν
θέσουμε x=1, τότε έχουμε:
τοξεφ(1) = π/4. Έτσι λοιπόν η σειρά (1), για
x = 1, δίνει:
Η
σειρά (3) αποτελεί και την πρώτη απειροσειρά
που βρέθηκε για το π. Όσο κι αν φαίνεται
παράξενο, ο ίδιος ο Gregory
δεν
έκανε ποτέ την αντικατάσταση x
= 1 και
έτσι δεν χρησιμοποιεί πουθενά αυτόν
τον
υπολογισμό
του π. Η
εφαρμογή της σειράς (1) του Gregory
για
x
= 1 (σχέση
3),
έγινε
από τον Leibniz
στα
1674 και δημοσιεύθηκε το 1682 και γι αυτό η
σειρά (3) ονομάζεται σειρά του Leibniz.
Ενδεχομένως
ο Gregory
να
είχε παρατηρήσει το πόσο πολύ αργά
συγκλίνει η σειρά του και γι αυτό να μην
θεώρησε σκόπιμο να την χρησιμοποιήσει
για την εύρεση του π. (Ο ίδιος είχε εισάγει
την έννοια της σύγκλισης). Για να
αντιληφθούμε το πόσο αργά συγκλίνει η
εν λόγω σειρά αρκεί να σκεφτούμε ότι
ακόμα και για τον προσδιορισμό των δύο
πρώτων δεκαδικών ψηφίων του π απαιτούνται
300 όροι της σειράς (Και να φαντασθεί
κανείς ότι η τιμή 3,14 είναι λιγότερο
ακριβής της τιμής 3 και 1/7 το Αρχιμήδη).
Ο
Thomas
De Lagny,
ο
οποίος υπολόγισε 117 ψηφία του π, ανέφερε
ότι για τον υπολογισμό 100 δεκαδικών
ψηφίων του π θα απαιτούνταν πάνω από
10^50 (1 ακολουθούμενο από 50 μηδενικά) όροι
της σειράς! Έτσι λοιπόν παρ όλη την
ομορφιά και την απλότητά της η σχέση
(3) είναι στην ουσία άχρηστη για τον
υπολογισμό των ψηφίων του π.
Βιβλιογραφία
- Αναφορές
David
Blatner, Η χαρά του π, (μετάφραση
του: The joy of π),
εκδόσεις Ωκεανίδα, Αθήνα 2001
Η ιστορία του
π, Παρασκευή Αρώνη, Μεταπτυχιακή
Διπλωματική εργασία,
http://www.math.uoa.gr/me/dipl/dipl_aroni.pdf
Γιάννης Φιορεντίνος
ΠΕ 04, ΜΔΕ Προχωρημένες Σπουδές στη Φυσική
(37) Συνεχίζεται...


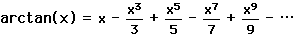
 (2)
(2)

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου