Τα 300 περίπου χρόνια που μεσολάβησαν ανάμεσα στην Αναγγέννηση και την Βικτωριανή εποχή, ήταν μια λαμπρή περίοδος για τα μαθηματικά. Αναφερθήκαμε ήδη στις επίμονες και επίπονες προσπάθειες του Van Ceulen στις αρχές του 17ου αιώνα για την εύρεση όσο το δυνατόν περισσότερων ψηφίων του π. Στη συνέχεια, μαθηματικοί όπως ο Viete, o Snellius και ο Huygens έστρεψαν το ενδιαφέρον τους από το κυνήγι περισσότερων ψηφίων στην εύρεση αποτελεσματικότερων τρόπων για τον υπολογισμό του αριθμού π. Ο Snellius και ο Huygens υπήρξαν οι (δύο) τελευταίοι μαθηματικοί που χρησιμοποίησαν την μέθοδο του Αρχιμήδη για τον υπολογισμό του π. [2]
ΠΕ 04, ΜΔΕ Προχωρημένες Σπουδές στη Φυσική
(36) Συνεχίζεται...
Ένας Άγγλος, σύγχρονος του Huygens, ο John Wallis (1616-1703), o οποίος ήταν μαθηματικός και κρυπτογράφος, εισήγαγε μια νέα μέθοδο για τον υπολογισμό του εμβαδού του κύκλου: Χρησιμοποιώντας απείρως μικρά ορθογώνια, προσπάθησε να προσεγγίσει το εμβαδόν ενός τεταρτοκυκλίου. Θεωρείται ότι είναι αυτός που πρώτος εισήγαγε το σύμβολο ∞ για το άπειρο.
Την εποχή του Wallis δεν είχε ακόμη επινοηθεί ο απειροστικός λογισμός και έτσι δεν υπήρχαν διαθέσιμα τα απαραίτητα εργαλεία (ταυτότητες, σύμβολα κλπ). Παρ' όλα αυτά, μετά από επίμονη και κοπιώδη προσπάθεια, στα 1655 και στο έγο του “Arithmetica Infinitorum”, κατάφερε να διατυπώσει τον τύπο, που φέρει το όνομά του:
Η σχέση του Wallis, όπως προηγoυμένως του Βιετ, είναι ένα γινόμενο άπειρων όρων (απειρογινόμενο), με τη διαφορά ότι ενώ στον τύπο του Βιετ εμφανίζονται (πολύπλοκες) τετραγωνικές ρίζες, σ΄αυτόν του Ουόλις υπάρχουν πράξεις μόνο μεταξύ ρητών αριθμών. Εκτός από αυτό ο τύπος του Ουόλις είναι ενδιαφέρων διότι συγκλίνει αργά προς το π. Ο πρώτος όρος είναι μεγαλύτερος (του π/2), ο δεύτερος μικρότερος, ο τρίτος και πάλι μεγαλύτερος κοκ. [1],[2].
Ο Viscount Brouncker (1620-1684) υπολόγισε μια τιμή για το π με την βοήθεια συνεχών κλασμάτων. Ο τύπος του, ισοδύναμος με αυτόν του Wallis, ήταν:
1. David Blatner, Η χαρά του π, (μετάφραση του: The joy of π), εκδόσεις Ωκεανίδα, Αθήνα 2001
Γιάννης Φιορεντίνος
Το συνεχές κλασμα παίρνει διαδοχικά τις τιμές:
1, 3/2, 15/13, 105/76, 945/789
Δεν είναι γνωστό πως κατέληξε στον τύπο του ο Brouncker. Ο Wallis απέδειξε την ισοδυναμία του τύπου του Brouncker με τον δικό του τύπο, μέσα από μια πολύπλοκη απόδειξη που μάλλον δεν πρέπει να ήταν ο δρόμος που ακολούθησε ο Brouncker. Αργότερα στα 1775, τον τύπο απέδειξε και ο διάσημος Ελβετός μαθηματικός Leonard Euler. [2]
Βιβλιογραφία - Αναφορές
1. David Blatner, Η χαρά του π, (μετάφραση του: The joy of π), εκδόσεις Ωκεανίδα, Αθήνα 2001
2. Η ιστορία του π, Παρασκευή Αρώνη, Μεταπτυχιακή Διπλωματική εργασία, http://www.math.uoa.gr/me/dipl/dipl_aroni.pdf
ΠΕ 04, ΜΔΕ Προχωρημένες Σπουδές στη Φυσική
(36) Συνεχίζεται...

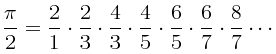



Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου