Με τον τετραγωνισμό του κύκλου, χωρίς όμως να συνεισφέρει στον υπολογισμό του π,
ασχολήθηκε και ο διάσημος ζωγράφος της αναγέννησης Albrecht Dürer (1471-1528).
Ενδιαφερόταν κυρίως για την προοπτική και τις αναλογίες στους πίνακες του
και έτσι ασχολήθηκε ερασιτεχνικά με τη γεωμετρία.
Στο έργο του “Underweysung der messung mit dem zirckel und rictsheyt ”
(“οδηγίες για τη μέτρηση με κανόνα και διαβήτη),
χρησιμοποιεί για τον αριθμό π, την τιμή π=3 και1/8,
δηλαδή την τιμή των Βαβυλωνίων.
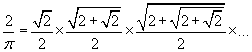
ασχολήθηκε και ο διάσημος ζωγράφος της αναγέννησης Albrecht Dürer (1471-1528).
Ενδιαφερόταν κυρίως για την προοπτική και τις αναλογίες στους πίνακες του
και έτσι ασχολήθηκε ερασιτεχνικά με τη γεωμετρία.
Στο έργο του “Underweysung der messung mit dem zirckel und rictsheyt ”
(“οδηγίες για τη μέτρηση με κανόνα και διαβήτη),
χρησιμοποιεί για τον αριθμό π, την τιμή π=3 και1/8,
δηλαδή την τιμή των Βαβυλωνίων.
Στην περίοδο που εξετάζουμε, η σημαντικότερη πρόοδος σε ότι αφορά τον υπολογισμό του π, οφείλεται στον Francois Viete (1540-1603).
O Viete, δικηγόρος στο επάγγελμα υπήρξε παράλληλα και σπουδαίος ερασιτέχνης μαθηματικός. Συνεισέφερε σημαντικά σε πολλούς κλάδους των μαθηματικών, όπως η Άλγεβρα, η Γεωμετρία, η Αριθμητική και η Τριγωνομετρία. Οι όροι “αρνητικός” και “συντελεστής”, οφείλουν την ονομασία τους στον Viete. Στις μελέτες του για τον υπολογισμό του π, βασίσθηκε στη μέθοδο του Αρχιμήδη και με κάποιες δικές του αλλαγές κατέληξε στην ακριβέστερη μέχρι την εποχή του τιμή για το π. [1]
O Viete, δικηγόρος στο επάγγελμα υπήρξε παράλληλα και σπουδαίος ερασιτέχνης μαθηματικός. Συνεισέφερε σημαντικά σε πολλούς κλάδους των μαθηματικών, όπως η Άλγεβρα, η Γεωμετρία, η Αριθμητική και η Τριγωνομετρία. Οι όροι “αρνητικός” και “συντελεστής”, οφείλουν την ονομασία τους στον Viete. Στις μελέτες του για τον υπολογισμό του π, βασίσθηκε στη μέθοδο του Αρχιμήδη και με κάποιες δικές του αλλαγές κατέληξε στην ακριβέστερη μέχρι την εποχή του τιμή για το π. [1]
Πιο συγκεκριμένα το 1579 ο Viete βρήκε για το π την προσέγγιση:
3,1415926535 < π < 3,1415926537
Για να το κατορθώσει, διπλασίασε τις πλευρές δύο εξαγώνων δεκαέξι φορές και υπολόγισε τις περιμέτρους εξάγωνων με 393.216 πλευρές το καθένα. Παρά το γεγονός ότι η τιμή που βρήκε για το π είναι ακριβής μέχρι 10 δεκαδικών ψηφίων, δεν θεωρείται το σπουδαιότερο επίτευγμα του. [2]
Το πραγματικό κατόρθωμα του Φρανσουά Βιετ ήταν το γεγονός ότι περιέγραψε το π μέσω ενός απειρογινομένου. Αυτό το επιτυγχάνει το 1593 στο βιβλίο του “Variorum de Rebus Mathematicis Resonsorum, Liber VIII (Διάφορα Μαθηματικά προβλήματα, τόμος 8). (Για περισσότερες πληροφορίες ο ενδιαφερόμενος αναγνώστης παραπέμπεται στην αναφορά [1]).
Σχέση του Viete για το π
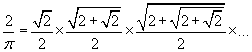
Από την εργασία: Η ιστορία του π, Παρασκευή Αρώνη, Μεταπτυχιακή Διπλωματική εργασία, http://www.math.uoa.gr/me/dipl/dipl_aroni.pdf
Ο Βιετ λοιπόν, όπως και πολλοί άλλοι σύγχρονοί του, χρησιμοποίησε τα αρχαία Ελληνικά μαθηματικά σε συνδυασμό με την Αραβική Άλγεβρα και την Τριγωνομετρία. Έτσι ενώ βασίσθηκε στην Αρχιμήδεια μέθοδο, κατάφερε να την εμπλουτίσει και να την εξελίξει κάνοντας χρήση της άλγεβρας και της τριγωνομετρίας. Γίνεται ο πρώτος που καταφέρνει να περιγράψει το π μέσω ενός απειρογινομένου. Δεν γνώριζε την έννοια της “σύγκλισης” και δεν τον απασχόλησε αν και κατά πόσο η άπειρη ακολουθία του συγκλίνει. Το ότι το απειρογινόμενο του Βιετ συγκλίνει, για πρώτη φορά αποδείχθηκε το 1891 από τον F. Rudio.
Βιβλιογραφία - Αναφορές
1. Η ιστορία του π, Παρασκευή Αρώνη, Μεταπτυχιακή Διπλωματική εργασία, http://www.math.uoa.gr/me/dipl/dipl_aroni.pdf
2. David Blatner, Η χαρά του π, (μετάφραση του: The joy of π), εκδόσεις Ωκεανίδα, Αθήνα 2001
3.
Άρθρο της Wikipedia: Francois
Viete
Γιάννης Φιορεντίνος
ΠΕ 04, ΜΔΕ Προχωρημένες Σπουδές στη Φυσική
(30) Συνεχίζεται...



Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου