Σχεδόν 19 αιώνες μετά το έργο “κύκλου μέτρησις” του Αρχιμήδη, άρχισαν οι έρευνητές του π να διερωτώνται για το αν υπάρχει κάποιος πιο σύντομος δρόμος, πέρα από τα πολύγωνα του Αρχιμήδη, για τον υπολογισμό των ψηφίων του π. Η μέθοδος της εξάντλησης με την οποία ασχολήθηκε ο Φαν Σόιλεν στα τελευταία χρόνια της ζωής του, λόγω των επίπονων και χρονοβόρων πράξεων (πολλαπλασιασμοί, διαιρέσεις, τετραγωνικές ρίζες που σχετίζονταν με εμβαδά πολυγώνων με δισεκατομμύρια πλευρές) ήταν άβολη και αποτρεπτική στο να χρησιμοποιηθεί και από άλλους ερευνητές. Έτσι ή θα 'πρεπε να αναζητηθούν νέοι καλύτεροι τρόποι για τον υπολογισμό των ψηφίων του π, ή θά 'πρεπε να παραμείνει κανείς ικανοποιημένος με τη γνώση λίγων δεκαδικών ψηφίων.
Τότε ακριβώς εμφανίζονται δύο σπουδαίοι Ολλανδοί μαθηματικοί, οι οποίοι κατάφεραν να βρουν ένα τέτοιο δρόμο και μάλιστα χωρίς την βοήθεια του απειροστικού λογισμού. Πρόκειται για τον Willebrord Snellius (Willebrord Snel van Royen, μαθηματικός, αστρονόμος και φυσικός 1580-1626 μΧ, ) και τον Christiaan Huygens ( μαθηματικός και φυσικός (1629-1695 μΧ).
Ο Snell ήταν καθηγητής στο πανεπιστήμιο του Leyden και στην ιστορία έμεινε γνωστός κυρίως για τη δουλειά του στη διατύπωση των νόμων της διάθλασης του φωτός.
(Για μια απόδειξη του νόμου του Snell, με βάση την αρχή του Fermat, ο ενδιαφερόμενος αναγνώστης παραπέμπεται στο:
Στα 1621 ανακάλυψε μια νέα μέθοδο για τον υπολογισμό του π, που ήταν έξυπνη και διόλου επίπονη. Στην προηγούμενη μέθοδο του διπλασιασμού των πλευρών ενός πολυγώνου, ο Snell αντέταξε ένα τρόπο για καλύτερη προσέγγιση του π, χρησιμοποιώντας μάλιστα τον ίδιο αριθμό (λίγων) πλευρών.
Κατασκευάζοντας απλά ένα εγγεγραμμένο εξάγωνο σε κύκλο, ήταν σε θέση να δείξει ότι το π πρέπει να βρίσκεται στο διάστημα:
3,14022 < π < 3,14160
Για σύγκριση, από ένα εξάγωνο, η τιμή του π που προκύπτει με τη μέθοδο του Αρχιμήδη είναι:
3 <π < 3,464
Η τιμή του π με την μέθοδο του Snell, είναι πιο ακριβής ακόμα και από την τιμή που προκύπτει με την Αρχιμήδεια μέθοδο για ένα 96-γωνο. Ενώ κάνοντας χρήση ενός 96-γώνου, ο Snell καταλήγει στην τιμή:
3,1415926272 < π < 3,1415928320
Με λίγη ακόμα προσπάθεια κατάφερε να επιβεβαιώσει τα 35 δεκαδικά ψηφία που είχαν ευρεθεί από τον (σύγχρονό του) Ludolph Van Ceulen και μάλιστα με πολύ πιο εύκολο και γρήγορο τρόπο.
Και βέβαια πέρα από αυτό καθ΄εαυτό το γεγονός του προσδιορισμού των ψηφίων, μεγάλη αξία έχει το γεγονός ότι εισήγαγε ένα νέο τρόπο υπολογισμού, την ορθότητα του οποίου επιβεβαίωναν τα ψηφία του π που προσδιόριζε. Δεν κατάφερε όμως να δώσει μια αυστηρή μαθηματική απόδειξη για τους ισχυρισμούς του.
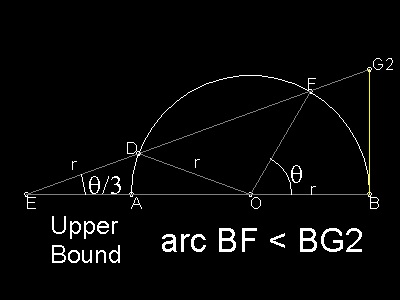
Το 1621 στο βιβλίο του Cyclometricus υποστήριξε ότι τα πάνω και τα κάτω όρια του π, όπως προκύπτουν από τα πολύγωνα του Αρχιμήδη, απέχουν πολύ εξ' αιτίας των ενδιάμεσων τόξων. Έτσι προσπάθησε να βρει όρια που θα προσέγγιζαν καλύτερα το μήκος ενός τόξου και τα κατάφερε. Όπως φαίνεται στο πρώτο από τα παρακάτω σχήματα, στην προέκταση της διαμέτρου ΑΒ, παίρνουμε το σημείο Ε, ώστε να είναι: ΒΕ=r (r, η ακτίνα του κύκλου). Ενώνοντας το F με το Ε (F σημείο τέτοιο ώστε γωνία ΒΟF= θ), παίρνουμε την FE που τέμνει στο σημείο G1 την εφαπτομένη του κύκλου στο σημείο Β. Θα είναι τότε: τόξο ΒF>BG1. Στο δεύτερο σχήμα, θεωρούμε ότι το σημείο D είναι τέτοιο ώστε DE=r, οπότε η γωνία DEA είναι ίση με θ/3, και στην περίπτωση αυτή τόξο ΒF<BG2.
Βιβλιογραφία - Αναφορές
David Blatner, Η χαρά του π, (μετάφραση του: The joy of π), εκδόσεις Ωκεανίδα, Αθήνα 2001
Η ιστορία του π, Παρασκευή Αρώνη, Μεταπτυχιακή Διπλωματική εργασία, http://www.math.uoa.gr/me/dipl/dipl_aroni.pdf
ΠΕ 04, ΜΔΕ Προχωρημένες Σπουδές στη Φυσική
(34) Συνεχίζεται...